Easily mistaken for the infinity sign, a circle or any number of more complex pretzels and knots, the Lissajous Figure is a picture of compound harmonic motion named for French physicist and mathematician Jules Antoine Lissajous (1822-1880). The shape is drawn by plotting a two-variable parametric equation as it iterates itself over time – the resulting figure is the picture of two systems falling into and out of phase.

In 1855 Lissajous constructed his "beautiful machine," devised to draw a picture of two systems superimposed and constructed in his Paris workshop of a pair of tuning forks placed facing at right angles, each with a mirror attached. The light source is focused through a lens, bouncing off the first onto the second and projecting to a large screen a few feet away. As the tuning forks are struck and tones are produced, simple vibrations begin to move the mirrors in a regular oscillating pattern. The projected image begins to form the strange and beautiful curves of a Lissajous Figure.

For his machine Lissajous was awarded the Lacaze Prize in 1873 and was exhibited at the Paris Universal Exhibition in1867. He did not otherwise distinguish himself as a scientist or mathematician. In fact, almost fifty years earlier American Nathaniel Bowditch had already produced similar figures with his harmonograph.

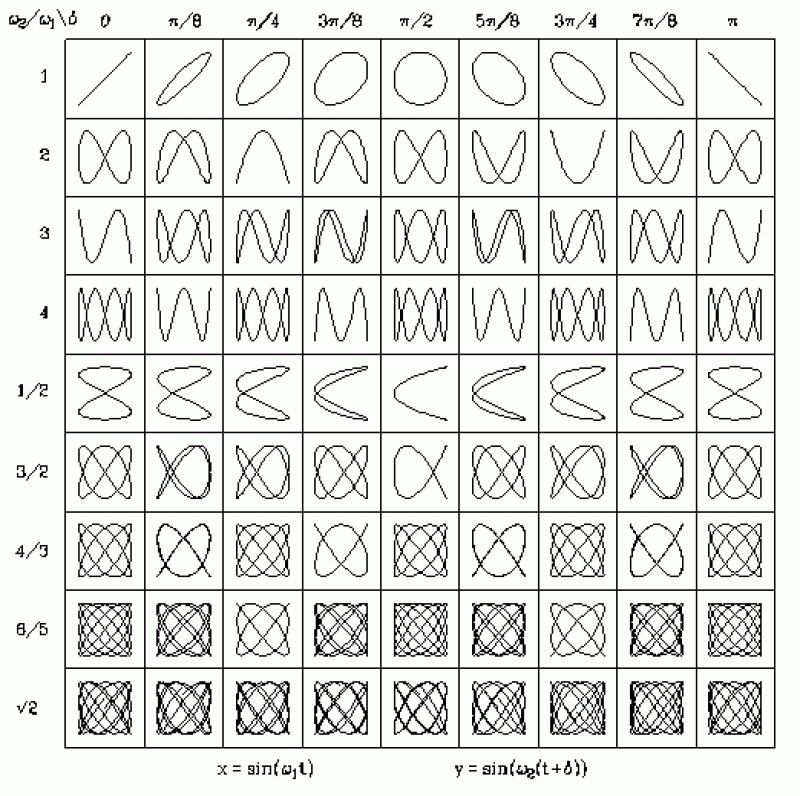
The simple harmonic motion which Lissajous was measuring is easily described by the motion of a clock's swinging pendulum. As the pendulum swings its speed isn't constant, but rather it accelerates and decelerates following a precisely predictable curve. If plotted over time, as the clock ticks the motion of its pendulum draws a sine wave – the so-called "pure wave" or zero-picture of a simple moving system. Ocean waves, sound waves, light waves, even average daily temperatures all produce this same oscillating sine wave pattern.

Compound harmonic motion, then, is simply the superimposition of two sine waves as they register, interfere and produce a series of overlapping waves. When juxtaposed at right angles, two sine waves recording simple harmonic motion produce the surprisingly complex figures that Lissajous identified.

Play

Sound Pattern 03

Sound and harmony made visible. Lissajous patterns made with 2 audio oscillators, a loud amplifier, plastic wrap, a bowl, and a laser pointer.

Lissajous Figures can be easily found today in computer graphics, in science museums, in laser light shows and, perhaps most precisely, burned into the green phosphor screen of a cathode-ray oscilloscope. A standard piece of electronic test equipment, the oscilloscope allows signal voltages to be viewed as a two-dimensional graph of potential differences, plotted as a function of time. When testing an electronic system, the phase differences between two signals form opposing sine waves on the screen of the oscilloscope connected together, constantly drawing and redrawing themselves in a precise and regular pattern.

These two varying signals produce a perpetual infinity (figuratively and literally as it will actually construct itself in the shape of the infinity sign given the right initial values). The Lissajous Figure becomes a picture of timing and sequence, registration and resonance, sound and music.

Specific shapes are produced corresponding to the resonating harmonic intervals familiar from western music (major fifth, minor third, major sixth, etc.) Any figure may be transformed into any figure and an infinite number of in-betweens as the oscillating sine waves pass in and out of harmonic resonance.

Jules Antoine Lissajous created a way to see sound (using mirrors, light and vibrating tuning forks.) But the most radical possibility of his mathematics might be in the commitment it asks of its audience. The image that Lissajous produces forms slowly right in front of your eyes — imperceptibly changing, forming, adjusting and re-aligning over time.

‘Who can does, who can not teaches!’ wrote Shaw. By this, he meant that if you were truly good at your trade, you’d rather practice that trade as a researcher rather than a teacher.

Many subjects are taught by professors who teach without any true engagement, who themselves have also been schooled by the very same sort of tutor. It might sound disrespectful, but it’s an undeniable phenomenon.

Most researchers have trained themselves with the guidance of another researcher.

How do you prevent the rift between researchers and teachers growing even wider? Firstly, by employing as many teachers as possible that have been successful researchers.

But also by writing textbooks, readers, and practical manuals in such a way that they show how research is truly done in a practical sense.

Most schoolbooks are written with present day knowledge as their foundation. They follow the history of their subject and its related disciplines from beginning to end. In textbooks, you won’t find many detours or examples of dead-end developments. And if that happens, you’ll know beforehand that it was a mistake. In practical manuals you won’t find experiments that explain a dead branch or root in history that helps understand the subject. Because of this, it seems like the subject developed through a succession of ready-made questions that lead to easily found answers. Knowledge and insight are taught on the basis of their justification.

But shouldn’t it also be possible to approach a subject through the history of its development? By not only looking at the grand scheme, but also at the crucial turning points? As a repetitive process of guessing, missing, and hitting. In the process of doing so, you’d be raising future researchers. And you’d be telling future teachers how researchers work.

If an idea to research something crazy suddenly befalls you, it’s well advised to go just through with it, complete it, and publish it. I once had the idea to visualise human coitus using an MRI scanner. It was a spontaneous idea; like the French poet-statesman Lamartine said, ‘I never think, my ideas think for me.’

I immediately received criticism. ‘What’s that good for?’ ‘You don’t even have a question! ‘We know everything already.’ But also enthusiasm: ‘if you want to research something that’s never been done, and easy as pie, do it! Why not?’

And so, we were able to conduct this study, but only in secret. Subsequently, the first scan was immediately compelling, iconoclastic even. It turned that all Da Vinci’s drawing proved to be fabrications, without anyone ever objecting (we and I included). The scans showed the previous depictions had originated partly from the bedroom (before death) and partly from the cutting table (after death).

The article about our research was rejected three times. That’s just how deviant our findings from the scanner were. Even our fourth article was considered to be ‘made-up’ by the British Medical Journal. The article wasn’t considered an actual report of an actual study until the magazine had done a thorough research on the accuracy of it, without us knowing. They even asked to include us in their Christmas edition (where every year strange studies are bundled).

Meanwhile, the study is the most clicked article on their site, while images of the scans weren’t even on the cover of the magazine. The film version of the MRI scan on the ‘Improbable Research’ site has been watched over a million times. It also immediately received the LG Nobel prize, because it makes one laugh before it makes one think.

In retrospect, the study is a classic example of Spielerei nebenbei to Ernst im Spiel and freedom in research.

Like Johan Huizinga argued in his Homo Ludens: play is indeed a higher order than severity because play includes severity, whilst severity excludes play.

In 1754, the British author Horace Walpole invented the term serendipity, describing it as "making discoveries, by accidents and sagacity, of things not in quest of". The name Serendip refers to The Princes of Serendip, a Persian fairy-tale in which three noble Persians from Sri Lanka made all sorts of unexpected observations that all turned out to be accurate.

The Three Princes of Serendip

The modern definition of serendipity is:

1) The talent to correctly interpret an unexpected observation and 2) the fruits of this talent.

In short, serendipity is the art of finding something you weren’t looking for, or the unplanned discovery itself. These can be “coincidental” discoveries, inventions or creations from science, technology or art; as well as unanticipated thoughts. In regards to serendipity, the word coincidental doesn’t correspond to the mathematical sense of randomness. Instead, it has a psychological meaning: something “falls to you,” often while you’re looking for something different.

One of these “coincidental” observations is usually the observable result of an (at that time) unknown cause. As soon as that unknown cause becomes known, the coincidental character of the observation disappears. Practice shows that it’s useful to interpret unanticipated observations as accurately as possible, especially if they contain the possibility of uncovering something grand. These wonderful observations can be seen as enigmas, anomalies, or novelties.

An enigma comprises of a mystery that no normal theory can explain. This was the case, for example, when the ancient Greeks observed, to their surprise, that amber attracts dust. By definition, an anomaly conflicts with accepted theory. When experiments showed that uranium cores could be split, this contradicted the prevailing belief that it was impossible to divide atoms. The idea could not be understood until the previous belief was dismissed. A novelty is different and does not conflict with accepted theories. Drais’ observation that he could use the steer of his pushbike to keep his balance was well within the mechanics of his time.

The Sophists knew that it’s impossible to actively look for the unknown, because you won’t know what it is you’re looking for. After all, nothing truly new can be derived from the old, because then it wouldn’t be really new. A surprise is needed; an exceptional observer or wondrous thought is needed to find something truly unknown.

Systematic searching and coincidental finding (serendipity) do not rule one another out. They compliment and intensify each another. Unintentional discoveries tend to be by catch. Of course, as long as you’re sitting on your bottom, you won’t stumble upon anything at all.

The “coincidental discovery” is rare. More common is the “coincidental observation” that is correctly interpreted. This demands previous knowledge. After all, you have to know what to expect in order to observe the unexpected as such. And correctly interpreting this demands knowledge and experience.

So, “expect the unexpected” (freely quoted from Heraclitus). And “readiness is all!” (Shakespeare) Poe commanded: “count on the unforeseen”!

Personal research. Fleming wrote beautifully about it: the researcher must be free to find new discoveries, wherever these may lead him. Every researcher needs a certain amount of personal time to work on his own ideas without having to justify them for anyone, unless he himself wishes to. After all, extraordinary ideas can form during one’s free time. The desire for immediate result is common, but can be detrimental. Truly valuable research is a long-term ordeal. In fact, it’s very possible that nothing of practical use emerges from a laboratory for years on end. Then, quite suddenly, something may appear. Something that is so innovative that its impact could cover the costs of the lab for a hundred years.

This bootlegging, this ‘playing in the boss’s time’ is zu lehren und zu lernen, at school and university, in theory and in practice. For example, you might soak peppercorns in water and ask students to observe them through a microscope to find out why they’re so sharp. Are they spiky? It then seems that something is moving under the microscope. Art there students who see this? If so, who? The participant is then asked to draw what they perceive. “You’ve only really seen something after you’ve drawn it,” Da Vinci wrote. Then you reveal that van Leeuwenhoek was also looking for spikes on peppercorns, unsuccessfully, and instead found what we now call bacteria. This experiment was done one my request in Amsterdam at a lyceum with success; the students were moved. This is how you uncover latent talent: by hiding unexpected findings in practical assignments, unannounced of course. The participants who missed the unexpected observations, or who did not pay enough attention, learned that they were insufficiently observant, surprised, flexible and active in comparison to their peers. Like behaviourist Skinner said, when you encounter something interesting, you must study that and leave the rest to wait.

The Hungarian endocrinologist Hans Selye so captivatingly wrote: ‘In my opinion, this is one of the most precious gifts for a scholar to enjoy. We tend to focus ourselves on what we are researching to the extent that other facts simply do not reach us, regardless if they are of far greater importance. This is mostly the case with things that deviate so greatly from the ordinary that they seem implausible. In the end, however, only the implausible is truly worthy of our attention.’